Sampling

Based on Chapter 7 of ModernDive. Code for Quiz 11.

1. Load the R packages we will use.

library(tidyverse)
library(moderndive)

2. Quiz questions

• Replace all the instances of ‘SEE QUIZ’. These are inputs from your moodle quiz.
• Replace all the instances of ‘???’. These are answers on your moodle quiz.
• Run all the individual code chunks to make sure the answers in this file correspond with your quiz answers
• After you check all your code chunks run then you can knit it. It won’t knit until the ??? are replaced
• The quiz assumes that you have watched the videos and worked through the examples in Chapter 7 of ModernDive

Question: 7.2.4 in Modern Dive with different sample sizes and repetitions

• Make sure you have installed and loaded the tidyverse and the moderndive packages
• Fill in the blanks
• Put the command you use in the Rchunks in your Rmd file for this quiz.

Modify the code for comparing different sample sizes from the virtual bowl

Segment 1: sample size = 30

1. 1. Take 1120 samples of size of 30 instead of 1000 replicates of size 25 from the bowl data set. Assign the output to virtual_samples_30

virtual_samples_30  <- bowl  %>% 
rep_sample_n(size = 30, reps = 1120)

1. 2. Compute resulting 1120 replicates of proportion red

• start with virtual_samples_30 THEN
• group_by replicate THEN
• create variable red equal to the sum of all the red balls
• create variable prop_red equal to variable red / 30
• Assign the output to virtual_prop_red_30

virtual_prop_red_30 <- virtual_samples_30 %>% 
  group_by(replicate) %>% 
  summarize(red = sum(color == "red")) %>% 
  mutate(prop_red = red / 30)

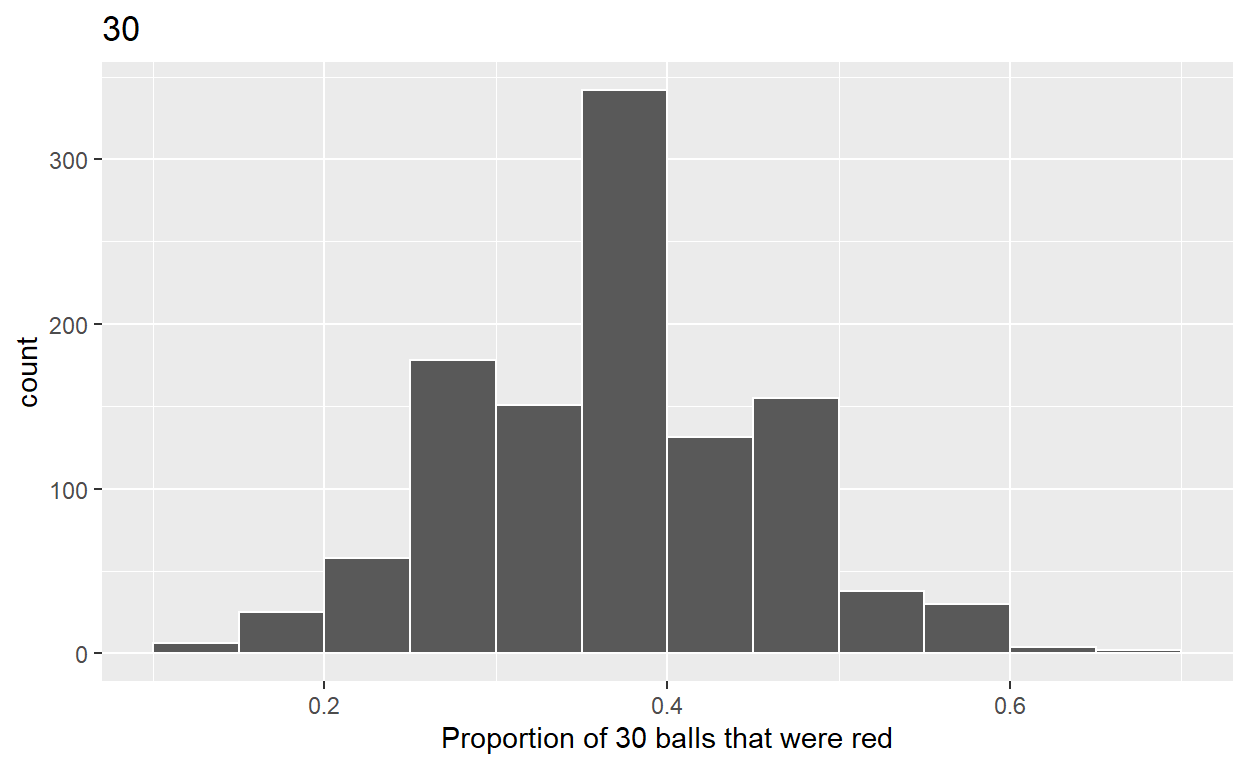
1. 3. Plot distribution of virtual_prop_red_30 via a histogram use labs to

• label x axis = “Proportion of 30 balls that were red”
• create title = “30”

ggplot(virtual_prop_red_30, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 30 balls that were red", title = "30") 

Segment 2: sample size = 55

2. 1. Take 1120 samples of size of 55 instead of 1000 replicates of size 50. Assign the output to virtual_samples_55

virtual_samples_55  <- bowl  %>% 
rep_sample_n(size = 55, reps = 1120)

2. 2. Compute resulting 1120 replicates of proportion red

• start with virtual_samples_55 THEN
• group_by replicate THEN
• create variable red equal to the sum of all the red balls
• create variable prop_red equal to variable red / 55
• Assign the output to virtual_prop_red_55

virtual_prop_red_55 <- virtual_samples_55 %>% 
  group_by(replicate) %>% 
  summarize(red = sum(color == "red")) %>% 
  mutate(prop_red = red / 55)

2. 3. Plot distribution of virtual_prop_red_55 via a histogram use labs to

• label x axis = “Proportion of 55 balls that were red”
• create title = “55”

ggplot(virtual_prop_red_55, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 55 balls that were red", title = "55") 

Segment 3: sample size = 114

3. 1. Take 1120 samples of size of 114 instead of 1000 replicates of size 50. Assign the output to virtual_samples_114

virtual_samples_114  <- bowl  %>% 
rep_sample_n(size = 114, reps = 1120)

3. 2. Compute resulting 1120 replicates of proportion red

• start with virtual_samples_114 THEN
• group_by replicate THEN
• create variable red equal to the sum of all the red balls
• create variable prop_red equal to variable red / 114
• Assign the output to virtual_prop_red_114

virtual_prop_red_114 <- virtual_samples_114 %>% 
  group_by(replicate) %>% 
  summarize(red = sum(color == "red")) %>% 
  mutate(prop_red = red / 114)

3. 3. Plot distribution of virtual_prop_red_114 via a histogram use labs to

• label x axis = “Proportion of 114 balls that were red”
• create title = “114”

ggplot(virtual_prop_red_114, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 114 balls that were red", title = "114")

ggsave(filename = "preview.png", 
       path = here::here("_posts", "2022-04-18-sampling"))

---

Calculate the standard deviations for your three sets of 1120 values of prop_red using the standard deviation

n = 30

virtual_prop_red_30 %>% 
  summarize(sd = sd(prop_red))

# A tibble: 1 x 1
      sd
   <dbl>
1 0.0893

n = 55

virtual_prop_red_55 %>% 
  summarize(sd = sd(prop_red))

# A tibble: 1 x 1
      sd
   <dbl>
1 0.0641

n = 114

virtual_prop_red_114 %>% 
  summarize(sd = sd(prop_red))

# A tibble: 1 x 1
      sd
   <dbl>
1 0.0448

The distribution with sample size, n = 114, has the smallest standard deviation (spread) around the estimated proportion of red balls.